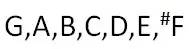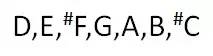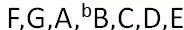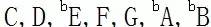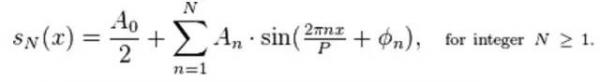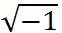| 音乐 数学 物理 老毕 和 二 |
| 送交者: 2023年04月16日21:06:39 于 [世界时事论坛] 发送悄悄话 |
|
|
|
文:华山 从那个很二的老毕说起 多年前,有一个很二的叫华山的人,发现了音乐的音阶其实并非基于12平均律,而是另外一种规律。他觉得这简直是革命性的发现。为了确保在告诉别人之前确认是前人没有做过的工作,他去查了资料。结果很受打击,因为在2600年以前,已经有一个叫“老毕”的人做了这个工作。2600年啊!都2600年过去了,你还重新发现,这不是重新发明轮子吗?
是的,是2600年以前的一个叫“老毕”的人发现并论证的。最近“老毕”这个名字很火,但是此“老毕”不是彼“老毕”,而是那个如雷贯耳的毕达哥拉斯!如果你现在还不知道这个毕达哥拉斯是干什么的,请立即停止阅读,回去重上初中。
此“老毕”不是彼“老毕” 说到这老毕,也就是毕达哥拉斯,我气就不打一处来。这小子先是毁了“勾股定理”的华夏发明权,现在又毁了林炎平的音阶发现权。 说到“勾股定理”,中国人都知道。兴许一些人也知道那其实是毕达哥拉斯首先证明的,因此实际上是“毕达哥拉斯定理”,因为这个老毕先给出了普遍的证明: a2+b2=c2 亦即:两个直角边的平方和等于斜边的平方。而我们华夏的祖先只是发现了“勾三股四弦五”,亦即:如果两个直角边分别是3和4,那么斜边就是5。但这只是直角三角形的一个特例,不是普适的充分必要条件。知道“普适”吗?知道“充分必要”吗?都是老毕和这些很二的古希腊人的理念。 老毕肯定是一个有钱的疯子:据说他为了这定理的证明花费了不少心血和时间,完了还宰了100头牛庆祝。你说你证明这干嘛呀?“勾三股四弦五”不就够了吗?再说埃及和两河流域的人更早就已经知道几十种构成直角三角形的边长关系,你费这么多的神整那个普遍的证明干嘛?还宰牛庆祝?不仅疯了,而且不轻。你不懂“民以食为天”吗?整这定理是能吃还是能喝? 老毕是疯子另一个证据是,他居然认为这个世界是由数组成的。他自己疯了还不够,还成立了一个学派,网罗了一群门徒,让大家和他一起发疯。因此他的学派里的弟子也都是疯子。你造吗?老毕有个弟子,觉得当时有关数的理论还不够疯,居然心怀不满。当时认为:所有的正数都可以表达为正整数组成的分数。也就是说,任何小数都可以表达为B/A(B比A)。这看起来很合理啊。比如: 1.5 = 3/ 2 1.33333… = 4 / 3 但这位弟子不这么认为,他有一天终于找到了别出心裁恶作剧的办法,证明了“根号二”不能表达为B/A。你说你和根号二过不去干嘛,不就是证明你比根号二还要二吗?啊?这二哥是这样证明的: 他用的是反证法,反正这个“反证法”也是这些疯子们发明的,这群疯子我们权且叫他们“希腊疯子”,因为那块地方那个时代盛产疯子,而别的地方找这样的疯子极其困难。 假设根号二可以表达为B/A,其中B和A都是正整数而且没有公约数。(假设很逻辑,他们那种疯子的特点就是很逻辑严谨想象力丰富。)亦即: √2 = B/A 那么 B2=2A2 你看见了吗?这公式里一共就6个符号,其中就有三个2,这就足够证明老毕和老毕学派有多么“二”了。好了,这小子继续: 因此,B一定是偶数(B的平方是偶数,那么B当然是偶数),于是可以将B表示为“2b”(b是正整数),你看见了吗?2b!又是一个二,而且是“二b”。无疑“2b”是那个时候开始的。我们继续,上式就变为: 4b2=2A2 亦即 A2=2b2 因此A也必定是偶数。由于A和B都是偶数,那么它们就有了公约数,于是和我们一开始的假设不符。因此,√2不可能表达为B/A。 结论:根号二不可能是有限循环小数。也就是说根号二是无限的不循环的小数。尼玛! 于是,“无理数”的概念诞生了! 你说这多二啊!简直令人痛心疾首啊!好好的世界就让老毕和他的门徒给毁了。本来好好的只有有理数的世界,从此没了。无理数啊!就这个名字就该多让人痛恨啊?老毕不是疯子是神马?毕达哥拉斯学派不是疯子是神马?那群希腊人不是疯子是神马?
那群“希腊疯子” 连老毕的另外一些徒弟都看不下去了,他们把这个发现无理数的小子扔进了爱琴海里,喝饱了水才捞上来,不知算是惩罚还是奖励,反正总归很二就是了。 但是世界上可能只记得疯子的事情,弄得2600年后的今天我们每人都学过这个证明,不过我们没有他那么二得不成样子,基本上学了也就忘记了。我们又回归正常了,又“民以食为天”了。记得以上证明的童鞋们请举手!没有?基本没有?这就对了。回去补习吧! 自从知道“毕达哥拉斯”定理后,我就恨上了老毕和古希腊。你整这个没用的干啥?你要是不整,700年后的东汉赵爽的证明不就拔了头筹吗?那样,“勾股定理”不就会是华夏的了吗?啊! 想不到更加痛恨的是后来。我以为发现了音乐音阶的秘密,结果一查,这老毕早就干过了,你说你2600年前整这事情干嘛?你说我现在整这事情是吃饱了撑的,还算有理由。你们那个时候吃穿都不富裕,居然不“以食为天”,却去整这些不能吃不能喝的。疯子,一群疯子!一群深井冰啊! 老毕的音阶理论 骂完了老毕,总也得描写一下当时的老毕都是如何发现音阶的秘密的。也顺便吹一吹林炎平是如何重新发现老毕早就发现的音阶构成的秘密的。 童鞋们,我们知道并不是所有频率的音都可以组成乐音。那么到底什么频率的音可以组成乐音呢?老毕是这样认为的: 如果音符1(do)的频率是f,那么上行1/2,也就是f乘以(1+1/2),就是另一个乐音,那就是5(so);(看见没有,又是2。如果你不足够二,到此为止,回去洗洗睡吧,不要再读下去了。)然后你再上行1/2,那就是2(re);继续,就是6(la);再继续,就是3(me);然后是7(si)。再继续,就是#4了。 当然也可以下行,1(do)的频率除以(1+1/2),就是4(fa);继续,就是降7(si);再继续就是降3(me)。 我们就暂时到这里,因为再继续,很多人就要疯掉了成为“深井冰”了。“深井冰”的意思就是“不断深入进行,然后越来越冰凉了”。就是这个意思。 老毕说,所有的乐音都是这样形成的。我们看看上面,实际上已经形成了所有大调音阶,1,2,3,4,5,6,7,甚至包括#4,b7和b3。 老毕说,为什么会是这样呢?因为1/2的音程是完全协和音,这样的音当然好听,因为协和或者叫和谐么。我们现在把这个1/2的频率音程叫做“纯五度”。 因为和谐(harmony)如此之好,对音乐如此重要,以致现在的交响乐团多用这个词根,称作“philharmonic”,亦即希腊语的“philia”(爱)加上希腊语的“harmony”(和谐)。听说过“柏林爱乐乐团”吗?就是这个词;听说过“卡拉扬”吗?就是这个乐团的“子飞”。记得这哥们的名言吗?“没有不好的乐团,只有不好的指挥。”意思就是好的子飞发现乐团里有人技术不行态度不对就直接开除了,不开除的限期达标,不达标的继续开除。啊?哦,其实不完全是这样,一个不是很出色的乐团在一个很好的指挥手里就成为了另外一个乐团。就如同不怎么会打仗的美国北非集团军到了巴顿手下就成了威武之师了。 和谐如此之好,好人坏人都要用;就比如科学(另外一个古希腊创造)如此之好,反科学的也要标榜自己科学。就如同冰箱席梦思抽水马桶如此之好,以致东方西方都要用,反西化的也用:白天声嘶力竭高喊反西化,晚上睡在席梦思上。慈禧太后当年没有冰箱,就只好在冬天库存很多冰供她夏天享用。如果有冰箱,叶赫那拉氏万岁万岁万万岁也肯定第一个用。于是和谐就变成现在的“河蟹”了,这解释了一个伟大的理念是如何被吃货贬值为食品的。至于抽水马桶,至今还有哪个国学卫道士蹲在茅坑上拉屎吗?
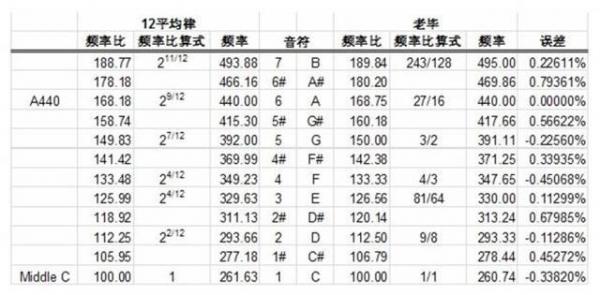
言归正传,如下是老毕方法的音阶相对频率和绝对频率表,以及12平均律的相对频率和绝对频率表。这是使得童鞋们变“二”的第一步,先不要管12平均律,那样会立即变疯的。我们的策略是逐步变疯:
表1:频率和音高的关系以及毕达哥拉斯音阶和12平均律音阶的误差 左列中的Middle C是钢琴上中间的那个C,那个A440是一个非常重要的音符,其是一个绝对音高,是后人规定的标准。就如同测量海拔一定要有海平面,没有它就不知道山峰的海拔高度了。而A440就是测量音阶的基准,所有别的音高都是根据它衍生的相对值。A440也就是大A音符,其频率定为440Hz。知道Hz吗?中文译作赫兹,是一个德国科学家的名字,为了纪念他而以此作为频率的符号。440Hz就是每秒震动440周。 如果记不住这个频率,就想想“二”,再看看这个440。440 = 2 X 220 这得多“二”啊!我相信你已经记住了。记住,如果不足够二,那么你既不能搞音乐,也不能搞数学,也不能搞物理。就这么简单。所以柏拉图当年的学园里必须要学数学和音乐,如果不懂数学那是绝对不合格的,因为你不懂数学和音乐就一定会成为一个坏人或者是蠢蛋。童鞋们,这是否有点太严厉?但是不能说人家不对吧? 老毕的麻烦 现在我们知道,“1”(do)乘以(1+1/2),就成了“5”(so),我们一直这样乘,就可以得到所有的音阶。
图表2:老毕音阶的上行和下行的误差 我这里只列出了自然音阶,加上
这就是老毕音阶的麻烦。本来这也没有什么,我们上行得到一部分音阶,除F(fa)以外,而下行得到F,就是完整的自然音阶了。最多再多上行和下行几步,就可以得到所有的12音阶。但是,这个环是不封闭的。也就是我们刚才看到的,上行得到的F和下行得到的F有大约2%的误差。 这本来是一个不是问题的问题,其并不影响我们对音乐的欣赏。但依旧是一件不完美的事情,尤其是对古希腊人,这样的不完美是不可容忍的。这不是由于在现实生活中对他们产生了什么负面的影响,一点都没有。但是从理论上,古希腊人不容忍这样的不完美。但是老毕无法解决它。老毕其实也没有试图采取任何妥协的方式来缓解它,因为对古希腊人来说,这样的妥协是不可容忍的。 但是这样的妥协在17世纪就变得十分现实了。特别在制作键盘乐器这样的有固定音阶的乐器的时候,上行的半音和下行的半音不相等就等于固定音阶的定位问题。比如, 12平均律的产生 正是这样的麻烦,导致了一个折衷的方案,毕竟,总不能为了这人耳无法辨别的2%频率误差再在A(6)和B(7)之间做出两个琴键(如果是钢琴的话)。用12平均律音阶代替老毕的音阶,实际上就是用可以容忍的错误代替过于麻烦的正确。在人类社会中这样的例子比比皆是。 现在我们回到图一来看看这些频率:老毕的参数和频率都是有理数,而12平均律的参数和频率(除了A440外)都是无理数。因此老毕的音程都是有理数,而12平均律的音程都是无理数。 老毕的音程生成是按照某一个主音的频率开始,然后不断乘以(1+1/2),就可以了。 12平均律就更加简单,其关键是一个参数21/12,亦即2开12次方,然后在某一个主音的频率上不断乘以这个参数即可。比如2(re)的频率,就是在1(do)的频率上乘以两次21/12,亦即22/12, 而5(so)的频率,就是乘以7次,亦即27/12。 那么这个21/12是如何产生的?实际上,“12平均律”就是把中音C和高音c之间的频率“平均”分成12个间隔,就是这样产生的,这也就是其名字的由来。但是这12等分不是算术等分,而是几何等分。也就是说,每一个音符的频率和前一个音符的频率之比例相等,而不是差额相等。我们根据这个原理,就可以计算这个比例:
即 p=21/12 这就是“十二平均律”的关键比例的由来。至于为什么相邻音符的频率增减的比例相同而不是增减的差额相同,这完全是由于我们的耳朵对音程的感觉和分辨。我们的感觉是和几何差距相关而不是和算术差距相关。比如我们对声音的强度就是如此,50分贝比40分贝实际上音强增加了10倍,50分贝比30分贝增强了100倍,但是我们感觉到的却是40分贝比30分贝所增强的和50分贝比40分贝所增强的是等值的。再比如,你在10岁的时候对一年的感觉,和你在50岁的时候对5年的长度感觉是一样的。所以小时候觉得一年很长,而大了以后觉得一年很短,越随着年龄增加,越觉得日子飞快。再比如涨工资,你一个月拿$1000的时候,给你涨$1000,那是什么感觉?简直是欣喜若狂。但是当你一个月拿$100,000的时候再给你涨$1,000,你肯定无动于衷甚至嗤之以鼻。贪得无厌就是这样来的,越多就觉得越不够多。紧跟多多益善的就是快快完蛋。 但是也有不贪的,那些很二的就属于这样的人。可喜的是,中国也有这样比较二的人。据说12平均律的最先提出者是中国明朝的皇孙朱载堉,他是明朝开国皇帝朱元璋的九世孙。如果真的是这样,那么朱载堉是中国皇家里最“二”的皇孙,和唐玄宗完全可以媲美。当然,在中国这些很“二”的都没有什么好的结局,唐玄宗弄了个安史之乱,连自己心爱的女人也没有保住。朱载堉也不可能当上什么皇帝。因此中国的问题是“二”的人没有什么好结局,因此“二”的人越来越少。不像希腊人,你不二,就不能独树一帜受人尊重。于是“二”的人越来越多。那个特别二的毕达哥拉斯只是众多二的哥们中的一个,你翻翻古希腊历史,真的找不出几个不二的来。
翻翻古希腊历史,真的找不出几个不二的来 比如那个更二的芝诺给出了一个悖论,楞是证明了他们祖上的国王和英雄阿喀琉斯追不上乌龟。你说要是在咱这里,你要是想说秦始皇追不上乌龟,你就全家玩完,你要是碰上汉武帝,你还没有说出来就被腹诽治罪满门抄斩了,到了康熙乾隆,你一句“清风不识字”刚写完,就让你变成青烟了。 反正,据说是朱载堉发明12平均律比西方早了几十年,还把21/12的计算精确到了25位数。如果属实,这还真的有一点祖冲之的精神。但是毕达哥拉斯没有这个兴趣,不仅毕达哥拉斯没有兴趣,到了阿基米德也没有对具体数值的兴趣。你要是穿越2000多年回去,问古希腊数学家√2的具体数值,他们肯定给你一个边长为1的正方形,然后画一条对角线,告诉你这条对角线就是√2。 尼玛。你能够说他不对吗,这可是最正确的√2。古希腊人对任何近似值都不感兴趣。阿基米德早就知道怎么算圆周率,但是这哥们算了几步就不算了,他的想法很清楚:反正我都知道这个方法了,具体计算没意思,只要你肯花功夫,多少位数都可以算到。这种计算工作在古希腊被认为是一种“蓝领工作”,被认为应该是奴隶们干的。
中国的皇帝都像朱载堉就好啦 总之,要是中国的皇帝可以像朱载堉这样比较二,把时间花在计算音阶的频率上而不是放在宫廷政变和抢班夺权和焚书坑儒上,中国的事情就会好办很多。中国问题就是在于皇帝不够二,子民也不够二,并且子民不喜欢二的皇帝。子民们总是为那些发动宫廷政变和权力斗争的胜利夺取皇位的阴谋家喝彩,而很少为那些没有政治野心而只是想把自己的兴趣玩好的个人喝彩。总之,这个民族不够二,太一,于是就有一个国家,一个皇帝,一个声音,一个思想,反正后来就成了一统天下,然后一筹莫展,最后就一塌糊涂了。人家很二,后来就二党制;咱们不二,就…… 调性与和弦 由于以上的原因,也就是由于我们的耳朵对于频率是否悦耳的判断,使得我们有了音阶。汉族的传统音阶比较简单,亦即所谓的五声音阶:1,2,3,5,6。没有4或7。别的民族的音阶可能比较复杂一些。西洋音阶不仅有4和7,而且经常有#4和b7。为什么#4和b7比较经常出现?因为它们最接近自然音阶:7(si)上行纯五度就是#4,而4下行纯五度就是b7。 尽管钢琴上的白键和黑键都是人为的,但是用来说明问题还是比较方便的。如果是C大调,那么就是以C为1(do)按照大调音阶生成的。在钢琴上就是全部白键。如果用绝对音高来表示,就是: C,D,E,F,G,A,B,这就是C大调的1,2,3,4,5,6,7(请对照图表一)。 但是我们并不想总是这样谱曲或者唱歌,比如一个人想把G当做1(do)来唱歌,这也没有什么不好。这时的绝对音高就会是这样的了:
这是由于,大调音阶要求在第六和第七音之间是一个全音,但是却碰到了E到F是一个半音的现实,于是不得不把F升半音,这样就解决了问题。 如果一个人想把D作为1来唱歌,那么音阶的情况就会是:
不仅F需要升半音,而且C也需要升半音。 那么有人想把F作为1来唱歌呢?这时音阶就变为:
我们看到自然音阶在第三和第四音之间需要是半音,而碰到的却是全音,于是就必须将B降半音。 如下是一个相当好用的办法,让你立即知道哪个调性需要有几个升降音,并知道升降哪几个音: 在一张纸上,先写1,2,3,然后把4,5,6,7错开插入,就变成: 4,1,5,2,6,3,7 或者写成绝对音高的形式: F,C,G,D,A,E,B 好了,我们开始。我们从C开始。C大调没有升降号。那么在C右侧的G大调呢?G的位置是C+1,这里的1就是我们要观察的左侧的第一个位置,也就是F。这意味着:G大调有一个升号,升在F上。不信你打开你们家的钢琴盖子,仔细核对一下。 D大调:这是在C+2的位置上,我们就取左侧两个音符,也就是F和C。这意味着:D大调有两个升号,升在F和C上。 如果是F大调,此时是C-1的位置,那么我们就取右侧第一个位置,这是B。因此,F大调有一个降号,降在B上。 如果我们再降一个调,但是我们发现F左侧已经没有东西了,此时我们就绕到右侧,第一个是B,由于是从左侧绕道右侧的,这个B实际上是
小调音阶和大调音阶的差别在于:其第三音总是降半音,而其第六音和第七音也经常降半音。如果审视一下C小调和C大调的区别: C小调为:
,而C大调是C,D,E,F,G,A,B。 按照我们以上的分析,c小调实际上是bE大调的音阶。于是,C小调和bE大调是很接近的。因此便有规律:一个大调和其下行小三度的小调拥有基本相同的音阶。比如C大调和A小调拥有基本相同的音阶。以此类推。 想知道贝多芬的九首交响曲用的是什么调式吗?
图表3:贝多芬的九首交响曲的调式 和弦又如何呢?由于这在维基百科上已经说得很多很好了,我和他们说的基本一致,因此就不必多说了。和谐给听众一种快感,这就是为什么音乐常常使用和弦。但是纯粹的完全的和谐却略显单调,比如对位和谐的是八度,比如C和c。拉过小提琴的人知道,当你在D弦上拉G这个音的时候,G弦(最里面的那根弦)会震动。而且振幅相当不小。这就是共鸣。 完全和谐是单调的,于是我们经常采用比较不单调的饱满的纯五度,也就是频率差为1/2的两个音符组成的和弦。比如C和G,这就比八度要饱满一些。但是这还不够,更加饱满的是大三和弦,也就是由三个音符组成,他们的音程是纯五度,大三度和小三度。这是一个十分明亮饱满的和弦。 再说,看到现在,你们头也大了。你们现在得出的结论不是音阶很容易,而是林炎平很二。但这不是林炎平的错,而是毕达哥拉斯的错,老毕才是始作俑者。 音域和音色 我们人的耳朵只能感知一定范围的声音频率,基本上就是在20Hz-20,000Hz。20Hz以下的叫次声,20,000Hz以上的叫超声,这两种声音我们都听不到。但是它们确实存在。次声对我们的健康有害,而超声有很多用途,比如医学上的B超成像检查,用的就是超声波。 乐器的频率非常有限,太低和太高的频率都令我们不悦,因此就不使用。比如我们的钢琴有88个键,其音域频率从最低的27.5Hz到4,186Hz。童鞋们不妨敲打一下钢琴上的最左侧和最右侧的键,已经可以感觉到太低和太高了。 钢琴确实音域很宽,有7个八度加4度,但是和耳朵可以听到的频率相比还是有限的。而我们人可以发出的声音频率就更加有限了。童鞋们可以一边敲钢琴的键,一边跟着唱,看看自己的音域有几个八度。如果你有一个半八度的音域,那就不错了。如果到两个八度,那就十分好了。如果可以到两个半八度,你就很有天赋了。不过记得不要在周围有人的时候试,免得把人吓跑了。也不要在夜深人静的时候试,免得有人报警,因为你努力唱高音的时候恐怕不会比喊救命更加优雅。
试试你能唱几个八度 如果你有两个八度的音域,而且发现你可以唱到C5,(亦即440 X 2 X 2= 1760Hz)那你是男高音,而且天份好极了。要是你可以唱到低音C2(亦即440/2/2=110Hz),那你就是男低音,并且值得骄傲了,因为中国人低音好的不多。如果你可以唱到C6,(亦即440 X 2 X 2 X 2 = 3,520Hz),那你就是很好的女高音了。
图表4:男低音和女高音的音域 我们可以看到,实际上男低音和女高音的音域实际上有一段是重合的。但是,为什么即便在重合的这一段,我们仍然可以分出哪个是男声,哪个是女声呢?这就是音色的不同造成的区别。这就如同我们很容易分辨小提琴、钢琴、小号、长笛的声音。它们可能发出的是同一个频率的音符,但是我们仍然很容易辨别是哪个乐器发出的。童鞋们,这是为什么呢? 当小提琴和长笛都奏出同一个频率的音符,比如C4(所谓Middle C)时,它们的基波相同,但是高次谐波却不相同。听起来这就是我们马上要进入直接从音乐爱好者变成疯子的节奏。在童鞋们变疯以前,我还是要再说几句。不想变疯的可以不听。 按照法国数学家傅里叶(Fourier,1768-1830)的发明和发现,任何一个振动都可以表述为数个或者无数个简谐振动的叠加。这里的所谓“简谐振动”就是正弦波振动。我们过去调钢琴的音高用的标准音叉产生的就是简谐振动,一个标准音叉只产生一种频率的简谐振动,而没有高次谐波,这样就避免由于高次谐波产生的一些不应该发生的共鸣的可能性。只有简谐振动可以做到这点,因为它没有高次谐波。 如下是傅里叶级数的表达式,说的就是上一段的意思。看到没有?N就是简谐振动的个数,它可以趋于无穷。
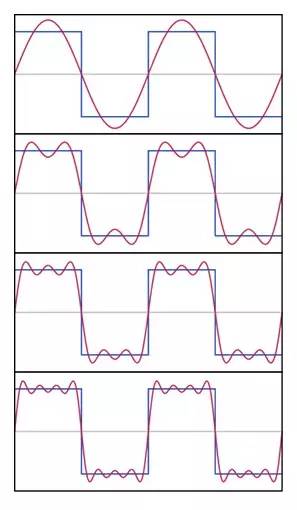
你相信吗,一个方形的波可以由无数个正弦波的叠加获得?我知道你不信,这就是你还没有变疯的证据。但是你很快就会变疯的。你看如下的图解:
图表5:一个方波可以由无数个正弦波叠加组成 图中蓝色的方形波在挑战我们的红色的正弦波:你要模仿我?你来啊! 好了,我们第一个正弦波(红色)来了,频率和方形波显然一样,两个波形的差距之大显而易见。很好,没有变疯。接着,第二个正弦波来了。这个正弦波具有两倍于方形波的频率以及较小的振幅,其和第一个正弦波叠加后,有那么一点点意思了。好像是方了一点?我是说疯了一点。接着再来第三个正弦波,其频率是方形波的三倍,振幅更小一些,以上三个正弦波叠加后显然波形更方了。我是说更疯了!经过四次叠加,我们就得到了一个相当方的波形。你还不信再叠加下去红色波形会越来越方并且最终和蓝色的方波彻底重合吗?傅里叶级数的误差分析就证明了:只要N趋向无穷,红波和蓝波之间的误差就趋于零。也就是说彻底重合。 我知道你已经变疯了!恭喜了!你向毕达哥拉斯迈进了一步。 现在我可以告诉你音色和音高的关系,以及音色的秘密了。那第一个正弦波,就是音高。后面所有的正弦波的叠加,就是音色!这就是你为什么可以听出长笛和小提琴的差别,这也是为什么你不会弄错男声和女声。 但是,未必。有的男声听起来像女声,反之亦然。这就是因为,由于某种原因他们的高次谐波也相同了。比如太监。 正是有了傅里叶级数,我们现在可以用电子合成任何乐器的声音。这就是你可以买一架电子琴,可以选择奏出各种乐器的声音。有电子琴吗?试试。合成的音色非常像原来的乐器,几可以假乱真。这就是用了傅里叶级数的原理,把钢琴的高次谐波加上去,你就听到了钢琴的声音;把小提琴的高次谐波加上去,你就听到了小提琴的声音。 令人不安和快乐的振动 振动既令人不安,也与人快感。如果你想到了地震和车震,那说明你还挺幽默。不过我们这里不说这个,只说广义的振动。 这种令人不安和与人快感的两难,却构成了某种人类创造文明的原动力。在不安和快感之间寻求某种平衡,是社会进步的一个重要途径。而音乐,正是这种进步的一个重要象征,亦即:让不安和快感产生刺激,却又达到和谐。这应该就是音乐的本质,也是人类社会进步的本质。 振动不可避免,英雄让振动成为音乐,并告诉你这样的美好可以通过理性获得;而枭雄让振动成为噪音,并告诉你这样的灾难不可避免。一个伟大的制度是让个体的振动保持足够的独立,并形成共同的和谐;而一个卑劣的制度是让所有个体都失去自由的振动,而让个别人去折腾所有个体。这就是为什么有的人群会有伟大的合唱,比如巴赫的大合唱,贝多芬的《欢乐颂》,而有的人群却只有在万马齐喑的集体静默和声嘶力竭的山呼万岁之间徘徊。 毕达哥拉斯在2600年前的那些对振动的研究,给我们带来了有关数学、物理和音乐之间关系的启迪。我不知道老毕当时把哪个作为他的优先级,数学?物理?音乐?我觉得这都不是他的所要追求的。他真正追求的是认识这个世界的奥秘。他把对世界本源的认识从具体的物质转向了抽象的概念:在物质的表象背后有着更加真实的本质,而这个本质可以不是物质的。在这个意义上,他超越了他的前辈泰勒斯和米利都学派。他是如此地极端,居然把世界和物质一刀两断,却把看不见摸不着的数认为是世界的本源,而物质只不过是其表象。以至于他的后来者德谟克利特的原子论几乎可以认为是泰勒斯们和毕达哥拉斯的思想的折衷。我不知德谟克利特是否真的折衷了毕达哥拉斯和泰勒斯,但是毕达哥拉斯充满勇气和智慧的论断应该足以让德谟克利特在提出世界万物都是由相同的不可再分的原子组成这一理论时少了一些犹豫。
老毕:追寻世界的本源 我相信当时老毕也是非常痛恨无理数的。但是那个出格的门徒正是由于老毕的精神才发现了无理数。我不知道老毕应该是感到骄傲还是沮丧,无论哪种,都是他那个学派的光荣和悲伤。他们的探讨如此深刻地影响了几千年后的人类社会。我不知道今天还有多少人在大学毕业20年后还会复述老毕和其门徒的证明,不少甚至忘记了老毕,但是老毕仔细论证过的音程和它们之间的和谐或者协和令我们绝大多数人心驰神往。很少有人对任何音乐都不感兴趣。 据说“不懂音乐的人的人格是不健全的”。我非常相信这点。尽管我觉得老毕很二很疯,正是有了这样的疯子,我们这个世界才变得理性和明亮起来。如果这个世界没有音阶,将会是个什么样子。我相信,没有毕达哥拉斯也会有音阶,也会有音乐。但是,如果没有了毕达哥拉斯这些人所代表的精神,人类对于音乐的理解可能就不会是后来的样子,而且那些伟大的作品未必会问世。 老毕的发现是极其基础的,基础到没有人在欣赏音乐的时候会想到他。但是,如果说柴可夫斯基的音乐是优美的散文,贝多芬的音乐是伟大的史诗,那么毕达哥拉斯的音阶和和弦就是文字和语法。没有了文字和语法,任何散文或史诗都不可能存在。我们在欣赏优美的散文和伟大的史诗时,很少会想到文字和语法,它们的存在似乎是天经地义的。但是,历史告诉我们:并非如此。记住毕达哥拉斯吧!正是他,给出了音乐的文字和语法。这是音乐无法撼动的基石和永恒的理念。 确实,振动带给了我们不安和快感。而和谐的音乐使得这种不安和快感升华为震撼心灵的天籁。我很愿意建议读者听贝多芬的第九交响曲以体验人类是如何将这种不安和快感登峰造极为如此伟大的音乐的。但是,在这里我却建议你在此时听一首很短小的曲子,其是众多伟大的曲子中的一首。我建议它,既是无意也是有意。请品尝和思考这首曲子。这就是Pachelbel(1653-1706)的“Canon inD”(D大调)。这是交响乐尚未问世的公元1700年以前的曲子。Pachelbel比巴赫早30年,比贝多芬早100多年。它是音乐作为文艺复兴的成果的重要代表。[1] 这首曲子和它的同时代的音乐一起,造就了巴洛克时代的音乐,也为巴赫和海顿铺平了道路,为贝多芬的登峰造极做好了准备。 贝多芬的音乐是令人极其不安的,它令人振奋,令人思索。他的音乐就是宣言:让令人不安和与人快乐的振动永远激励我们! 那些美丽背后的数学 我们介绍了Canon in D,其实,Canon并不是这首乐曲的名字,而是一种规则,Canon in D的意思是用Canon这个规则写的D大调乐曲。Canon是音乐应该尊重的完美的规则,并且,Canon作为一种美学规则,也不仅仅用于音乐,同样可以用于绘画。而实际上,Canon在绘画上的运用要比在音乐上早得多。 文艺复兴的绘画在艺术领域里最先体现了人本主义精神。波特切利在1482年创作的《春》和1486年创作的《维纳斯的诞生》是这个伟大新时代的先驱[2]。在这里也顺便纪念一下吧。插图是这幅画的局部,当代好事者在画面添加的斐波那契级数地砖(Fibonacci Tiles)是为了说明Canon在绘画审美上的运用。 Pachelbel在此200年后创作的Canon in D,似乎是音乐对绘画先驱们的一个回音。至于为什么文艺复兴的精神在音乐上的体现要比在绘画上晚了200多年,这是一个很有趣的问题。到底为什么音乐的进步滞后于其它艺术的进步?这仅仅是中世纪走向文艺复兴的一个特例?还是一个普遍的规律?希望大家来寻找这个答案。 在公元前800年,古希腊的行吟诗人荷马在希腊城邦间云游的时候,我们今天只知道他吟诵的内容,以及使用的乐器,但是并不知道他吟唱的旋律。那些旋律永久消失在历史的尘埃里了,而这些史诗所传唱的古希腊理念却在希腊地区形成了共同的文化和价值,进而产生了独特的民主政治和自由理念。如果没有荷马和他的史诗,我相信古希腊不会有泰勒斯和赫拉克利特,也不会有梭伦以及后来的克里斯蒂尼和伯里克利,也不会有苏格拉底、柏拉图和亚里斯多德,也不会有埃拉托色尼和阿里斯塔克。当然,也不会有毕达哥拉斯。介于荷马史诗的传唱和此后城邦政治的繁荣之间的毕达哥拉斯和他的学派到底起了什么作用?这也许是一个无法彻底在这里讨论清楚的问题。但是,我们可以肯定,毕达哥拉斯的意义跨越了当时的空间也跨越了此后的时间。
图表6:波特切利的《维纳斯的诞生》局部和可能的斐波那契级数的审美意义(Canon)[3] 古希腊和毕达哥拉斯时代的音乐已经不可考了,音乐不像建筑,后者几乎与世长存,但是前者却瞬时即逝。但是伟大的音乐一定以其的深厚和振奋把自己凝固在当时的建筑中,我相信任何时代的建筑都体现了那个时代的音乐。音乐是流动的建筑,而建筑则是凝固的音乐。音乐是振动在时域中表现的动感,而建筑是振动在频域中表现的静态。(我这里提到了“时域”和“频域”,这是两个术语,不谙数学物理的童鞋可以不理会它们,只要知道“时域”是关于动态时间的坐标,“频域”是关于固定频率的坐标。) 毕达哥拉斯证明了音乐和数学物理之间有着非常紧密的关系,这和“毕达哥拉斯”定理的意义同样深远。 如果没有数学,也就不会有物理。没有了数学和物理,人类社会还剩下什么?洪荒一片,这而绝非危言耸听。而没有了数学规律,也就没有了音乐,人类社会将只有噪音。 音乐一定是通过数学和物理更加长久地成为我们人类精神上的永久建筑。 数学、音乐和物理同样重要,这就是为什么在毕达哥拉斯之后2000年,文艺复兴时代的伽利略如是说“上帝是通过数学创造了宇宙”。他的时代还不能接受他真正想说的话“只有数学不可怀疑”。这是毕达哥拉斯“数是万物之源”在2000年后的伟大回音和共鸣。 如果以上写的让你对音乐的物理数学原理有了一点了解,让你有了一些探讨音乐背后的理念的理由,让你对音乐本身有了一些兴趣,那就请你谢谢毕达哥拉斯吧! 毕达哥拉斯幽灵
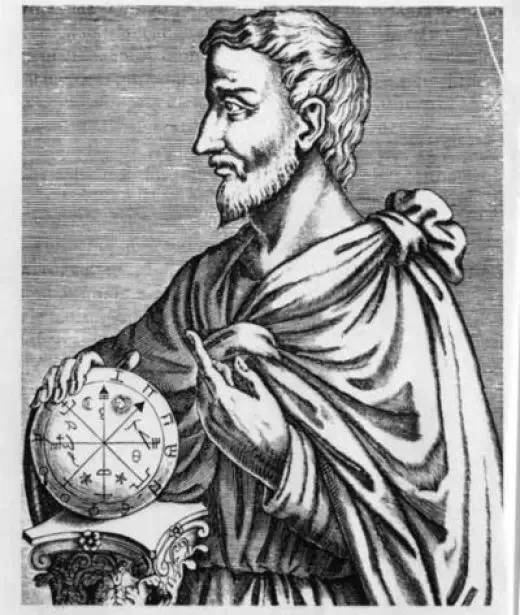
我们这个世界只是数的规律的表象。毕达哥拉斯肯定会说这句话。 在毕达哥拉斯的那个弟子发现了无理数之后的2000年,人们又发明了另外一个更加不可思议的数,这就是虚数。我在这里之所以说无理数是“发现”,而虚数是“发明”,这是因为无理数是自然存在的,而虚数是我们为了使用而发明的。当然你也可以争辩:其实所有的数都是发明的。虚数的单位是 。我知道你肯定说发明这个的人比毕达哥拉斯的那个弟子还要“二”。确实,-1是没有平方根的,但是为什么我们不制造一个平方根,规定它的平方就是“-1”?你不开心吗?那你就不开心吧。 事实证明,这个的作用极大,使得原来的数一下子从一维扩展到了二维。你这会看出来了,“二”又来了。没有了这个虚数,拉普拉斯变换也就不可能产生,没有了拉普拉斯变换,电子学电工学和控制论都可以歇菜了。因此我们看到,数学是多么伟大。伽利略没有错,毕达哥拉斯没有错。 这些都太枯燥了,这样下去真的读者都跑光了。你如果现在还没有跑掉,那么你已经是那5%坚持到最后的。先别跑,这就结束了。 但是在结束前,我们一定要给大家看一个伟大的方程,这就是欧拉方程。 我们知道,在所有的数中,有5个是最重要的常数,它们是:0,1,π(圆周率3.141592…),e(自然对数的底2.718281828…), e 你还不相信上帝通过数学创造了宇宙吗?如果你还不信,那么我们来看一下“黄金分割”和“斐波那契级数”。黄金分割和斐波那契级数其实是一回事。看过《达芬奇密码》的人一定知道斐波那契级数,那是文艺复兴前夕的意大利数学家斐波那契(Leonardo Fibonacci 1170 - 1250)发明和发现的。 斐波那契级数是这样的: 1,1,2,3,5,8,13,21……Fn 其中 Fn=Fn-1+Fn-2, 黄金分割则是由古希腊人发现的,也和毕达哥拉斯有关,欧几里得对其是这样定义的: 将某个长度切成两部分,使得整体比长局部等于长局部比短局部,那么这个比例就是黄金分割。求解可以获得这个比例
有意思的是,在斐波那契级数中,后一项和前一项的比,随着n的增加,总是在黄金分割值上下浮动,而且逐渐接近黄金分割值,最后在n趋于无穷时收敛于黄金分割值。 上面我们提到了欧几里得。这是一位在毕达哥拉斯之后的“二”的集大成者。他的《几何原本》在2000多年后的今天还在原封不动地作为教科书教导我们。欧几里得几何是“普世价值”的最好诠释,不管你是什么民族什么地位什么肤色什么信仰,你都必须学习欧几里得几何。(当然你可以说还有“非欧几何”,亦即“双曲几何”和“椭圆几何”。没错,这是欧几里得几何的两个“孙子”,但这是另外一回事,这里就不多说了。)欧几里得几何是逻辑思维的榜样和科学方法的典范。
顺便说一句,欧几里得用不到10行字词,就证明了素数的个数是无穷的。有兴趣的自己查找,那方法绝妙无比,用的也是我们开篇举例中的“反证法”,实在是精彩绝伦光辉夺目,这里不予展示,免得亮瞎你的双眼。 当代的“好事之徒”们认为斐波那契级数和黄金分割是伟大画家们实际遵守的规则,不管是有意识的还是下意识的。那个海螺式的图形就是所谓斐波那契级数“地砖”。他们号称波特切利和达芬奇就是按照这个规则构图的,因此这是美术的Canon。 至于达芬奇,这是一位我们不需要讨论的人。他是伟大的画家,这是大家都知道的,《蒙娜·丽莎》和《最后的晚餐》都是大家耳熟能详的。但他还是工程师、生物学家、解剖学家、建筑师……,还有,他是一位出色的数学家。看到没有?数学!看到毕达哥拉斯的影子了吗?这位伟大天才的事迹和创造实在太多太精彩,建议童鞋们找来看看。
图表7:达芬奇的绘画和手稿 我刚才提到了毕达哥拉斯的“影子”,那其实不是影子,而是幽灵。这是毕达哥拉斯幽灵,一个古希腊幽灵,诞生于古希腊的爱琴海,穿越过漫长的中世纪,发轫于文艺复兴时代,滥觞于我们现代。我们到处都有这样幽灵,到处都受惠于这个幽灵,比如自由平等博爱民主科学公民。当然包括我们说的音乐数学物理,还有绘画。这个幽灵的副作用就是很“二”,它根本不知道“以食为天”,从不安分守己,时刻异想天开,到处寻衅滋事。 我想说的是,如果你喜欢音乐,请向毕达哥拉斯致敬,向“二”致敬。如果你不喜欢音乐,那么是你开始喜欢音乐的时候了。因此,也是你开始喜欢毕达哥拉斯和他的幽灵的时候了。 - End - [1]:https://www.youtube.com/watch?v=JvNQLJ1_HQ0(PachelbelCanon in D Major - the original version)国内的朋友只好在别的音乐网站上找,或者直接在iTune上下载。 [2]https://artislimited.wordpress.com/2012/10/03/the-canons-of-beauty-in-the-history-of-art-the-golden-mean/ [3]参见卡农的美学意义 http://en.wikipedia.org/wiki/Aesthetic_canon |
|
|
 |
 |
| 实用资讯 | |
|
|
| 一周点击热帖 | 更多>> |
| 一周回复热帖 |
| 历史上的今天:回复热帖 |
| 2022: | 从语言比较看中西方思维和文化的差异 | |
| 2022: | 大难临头,只有毛泽东可以救中国 | |
| 2021: | 中共疫苗是垃圾! | |
| 2021: | 俄罗斯怒怼日本,福岛核废水到底有没有 | |
| 2020: | 对疫情的一些想法 | |
| 2020: | 关于被喝茶的经验分享及推特安全 | |
| 2019: | 30周年祭| 胡耀邦的最后7天 | |
| 2019: | 大卫·哈维:天下资本一般黑,中国没有 | |
| 2018: | 不怕不识货,就怕货比货 | |
| 2018: | 犯鸿茅药酒者,虽远必诛 | |